-
Notifications
You must be signed in to change notification settings - Fork 250
[Utilities] MMG Process
MMG is an open source software for simplicial remeshing. MMG main page, and you can download the code in GitHub.
-
It provides 3 applications and 4 libraries:
- The
mmg2dapplication and thelibmmg2dlibrary: adaptation and optimization of a two-dimensional triangulation and generation of a triangulation from a set of points or from given boundary edges - The
mmgsapplication and thelibmmgslibrary: adaptation and optimization of a surface triangulation and isovalue discretization - The
mmg3dapplication and thelibmmg3dlibrary: adaptation and optimization of a tetrahedral mesh and implicit domain meshing - The
libmmglibrary gathering thelibmmg2d,libmmgsandlibmmg3dlibraries
- The
-
It uses a LGPL license and it has been integrated in Kratos via the
mmg_process.hin theMeshingApplication. Important: For use it you need to download first (look in the installation section) -
It is used like a process, using the
mmg_process.pyin theMeshingApplication. -
There are basically two different types of re-meshing strategies (both of them compatibles with an anisotropic re-meshing):
-
Level-Set: This re-meshing technique is based in the gradient of theDISTANCEfunction, and can be used to re-mesh when you are getting closer to the reference geometry. -
Hessian: This re-meshing technique is based in the computation of the Hessian of any variable, in the case of more than one variable or a variable by components is considered them the intersection of the corresponding tensors is computed.
-
The installation of the library is fortunately quite straightforward thanks to the marvels of the configure scripts. The easiest way is the following one, because requires the minimal effort; of course if you have expertise you can find an alternative way to install the library:
- Go to
MeshingApplication/custom_external_libraries/- Here you can see the
mmgfolder, but it is empty. You have theREADME.txt, where the installation is explained, and the build folder, where theconfigure.shscript can be found. - Go to a folder of your chose to install the library (for example
~/src) (make sure you have installedgitfirst):
- Here you can see the
git clone /~https://github.com/MmgTools/mmg.git- Then copy the
buildfolder from the oldmmgfolder to the newmmgfolder. Go to the build folder and execute:
Linux
sh configure.shWindows (Command prompt)
configure.batWindows (Powershell)
./configure.bat- Once the compilation is done go to the main Kratos folder and go to your
scriptsfolder. Here you modify theconfigure.shorconfigure.batadding the following lines (modify thekratos_dirfor your current Kratos installation directory):
-DINCLUDE_MMG=ON \
-DMMG_ROOT="/path/to/src/mmg/build" \It will be assumed that the libraries folder is under /path/to/srtc/mmg/build/lib. In case your libraries are not detected automatically, you can specify the path by using:
-DINCLUDE_MMG=ON \
-DMMG_BUILDDIR="/path/to/src/mmg/build" \
-DMMG_LIBDIR="/path/to/custom/mmg/lib" \In Windows, it is possible that the build folder was written in your C://Program Files/ folder
Further information and possible errors are covered in this README.
- After that recompile Kratos using again: Linux
sh Kratos/scripts/configure.shWindows
Kratos/scripts/configure.shGo to the folder tests in the MeshingApplication and run:
python3 test_MeshingApplication.pyYou should get an OK, if you don't get an OK there is something wrong:
- Check that your compilation is the correct one
- Follow again all the steps
- Check that the configure.sh it is correctly compiled
- If you get an
Unexpected error:- This problem is because your machine is not compatible with the library, unfortunately this means that you need to wait until the problem is solved
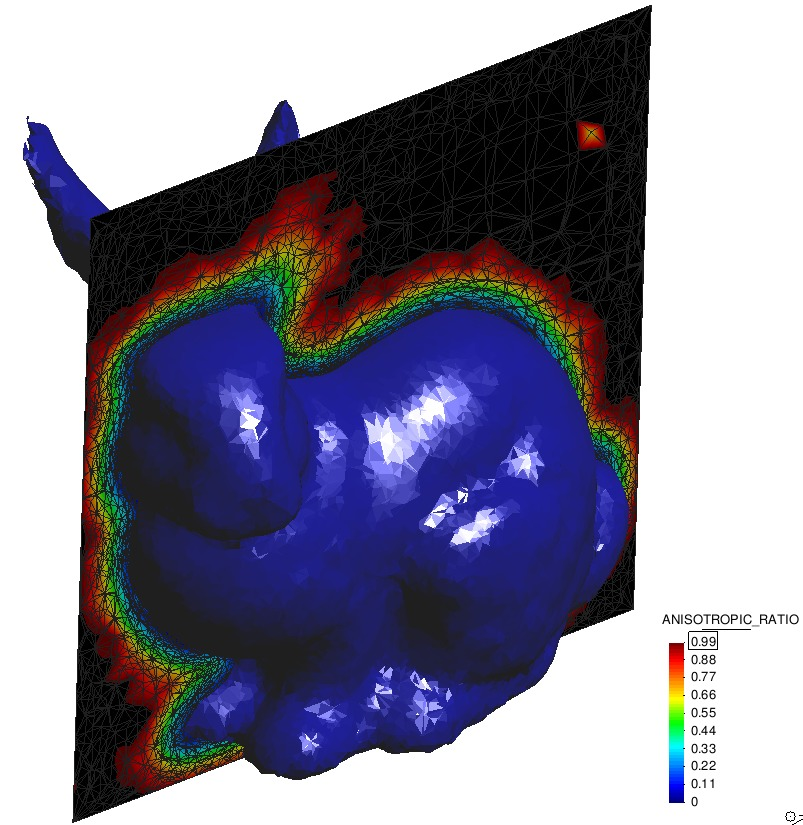
Taking for example the following mesh, and using the following python script (included in the previous compressed file) it is possible to re-mesh a very coarsed mesh of a sphere into a fine an anisotropic sphere.
from __future__ import print_function, absolute_import, division #makes KratosMultiphysics backward compatible with python 2.6 and 2.7
import KratosMultiphysics
import KratosMultiphysics.MeshingApplication as MeshingApplication
current_model = KratosMultiphysics.Model()
main_model_part = current_model.CreateModelPart("MainModelPart")
main_model_part.ProcessInfo.SetValue(KratosMultiphysics.DOMAIN_SIZE, 3)
# We add the variables needed
main_model_part.AddNodalSolutionStepVariable(KratosMultiphysics.DISTANCE)
main_model_part.AddNodalSolutionStepVariable(KratosMultiphysics.DISTANCE_GRADIENT)
main_model_part.AddNodalSolutionStepVariable(KratosMultiphysics.NODAL_AREA)
# We import the model main_model_part
KratosMultiphysics.ModelPartIO("coarse_sphere").ReadModelPart(main_model_part)
# We calculate the gradient of the distance variable
local_gradient = KratosMultiphysics.ComputeNodalGradientProcess3D(main_model_part, KratosMultiphysics.DISTANCE, KratosMultiphysics.DISTANCE_GRADIENT, KratosMultiphysics.NODAL_AREA)
local_gradient.Execute()
# We set to zero the metric
ZeroVector = KratosMultiphysics.Vector(6)
ZeroVector[0] = 0.0
ZeroVector[1] = 0.0
ZeroVector[2] = 0.0
ZeroVector[3] = 0.0
ZeroVector[4] = 0.0
ZeroVector[5] = 0.0
for node in main_model_part.Nodes:
node.SetValue(MeshingApplication.METRIC_TENSOR_3D, ZeroVector)
# We define a metric using the ComputeLevelSetSolMetricProcess
level_set_param = KratosMultiphysics.Parameters("""
{
"minimal_size" : 0.1,
"enforce_current" : false,
"anisotropy_remeshing" : true,
"anisotropy_parameters":
{
"hmin_over_hmax_anisotropic_ratio" : 0.01,
"boundary_layer_max_distance" : 0.5,
"interpolation" : "Linear"
}
}
""")
metric_process = MeshingApplication.ComputeLevelSetSolMetricProcess3D(main_model_part,KratosMultiphysics.DISTANCE_GRADIENT,level_set_param)
metric_process.Execute()
# We create the remeshing process
remesh_param = KratosMultiphysics.Parameters("""{ }""")
MmgProcess = MeshingApplication.MmgProcess3D(main_model_part, remesh_param)
MmgProcess.Execute()
# Finally we export to GiD
from gid_output_process import GiDOutputProcess
gid_output = GiDOutputProcess(main_model_part,
"gid_output",
KratosMultiphysics.Parameters("""
{
"result_file_configuration" : {
"gidpost_flags": {
"GiDPostMode": "GiD_PostBinary",
"WriteDeformedMeshFlag": "WriteUndeformed",
"WriteConditionsFlag": "WriteConditions",
"MultiFileFlag": "SingleFile"
},
"nodal_results" : []
}
}
""")
)
gid_output.ExecuteInitialize()
gid_output.ExecuteBeforeSolutionLoop()
gid_output.ExecuteInitializeSolutionStep()
gid_output.PrintOutput()
gid_output.ExecuteFinalizeSolutionStep()
gid_output.ExecuteFinalize() The metric can be calculated by hand if you prefer, for example to get the same result than the previous script:
# We import the libraies
from __future__ import print_function, absolute_import, division #makes KratosMultiphysics backward compatible with python 2.6 and 2.7
import KratosMultiphysics
import KratosMultiphysics.MeshingApplication as MeshingApplication
# We create the model part
current_model = KratosMultiphysics.Model()
main_model_part = current_model.CreateModelPart("MainModelPart")
main_model_part.ProcessInfo.SetValue(KratosMultiphysics.DOMAIN_SIZE, 3)
# We add the variables needed
main_model_part.AddNodalSolutionStepVariable(KratosMultiphysics.DISTANCE)
main_model_part.AddNodalSolutionStepVariable(KratosMultiphysics.NODAL_H)
# We import the model main_model_part
KratosMultiphysics.ModelPartIO("coarse_sphere").ReadModelPart(main_model_part)
# We know that the gradient is unitary and in X direction
UnityVector = KratosMultiphysics.Vector(3)
UnityVector[0] = 1.0
UnityVector[1] = 0.0
UnityVector[2] = 0.0
# We set to zero the metric
MetricVector = KratosMultiphysics.Vector(6)
for node in main_model_part.Nodes:
# Calculate the element size
distance = node.GetSolutionStepValue(KratosMultiphysics.DISTANCE, 0)
nodal_h = node.GetSolutionStepValue(KratosMultiphysics.NODAL_H, 0)
element_size = 0.1
if (abs(distance) > 0.5):
element_size = nodal_h
# Calculate anisotropic ratio
ratio = 1.0
if (abs(distance) < 0.5):
ratio = 0.01 + (abs(distance)/0.5) * (1.0 - 0.01);
# We get the gradient
gradient_value = UnityVector
# Finally we calculate the metric
coeff0 = 1.0/(element_size * element_size);
coeff1 = coeff0/(ratio * ratio);
v0v0 = gradient_value[0]*gradient_value[0];
v0v1 = gradient_value[0]*gradient_value[1];
v0v2 = gradient_value[0]*gradient_value[2];
v1v1 = gradient_value[1]*gradient_value[1];
v1v2 = gradient_value[1]*gradient_value[2];
v2v2 = gradient_value[2]*gradient_value[2];
MetricVector[0] = coeff0*(1.0 - v0v0) + coeff1*v0v0
MetricVector[1] = coeff0*(1.0 - v1v1) + coeff1*v1v1
MetricVector[2] = coeff0*(1.0 - v2v2) + coeff1*v2v2
MetricVector[3] = coeff0*( - v0v1) + coeff1*v0v1
MetricVector[4] = coeff0*( - v1v2) + coeff1*v1v2
MetricVector[5] = coeff0*( - v0v2) + coeff1*v0v2
node.SetValue(MeshingApplication.METRIC_TENSOR_3D, MetricVector)
# We create the remeshing process
remesh_param = KratosMultiphysics.Parameters("""{ }""")
MmgProcess = MeshingApplication.MmgProcess3D(main_model_part, remesh_param)
MmgProcess.Execute()
# Finally we export to GiD
from gid_output_process import GiDOutputProcess
gid_output = GiDOutputProcess(main_model_part,
"gid_output",
KratosMultiphysics.Parameters("""
{
"result_file_configuration" : {
"gidpost_flags": {
"GiDPostMode": "GiD_PostBinary",
"WriteDeformedMeshFlag": "WriteUndeformed",
"WriteConditionsFlag": "WriteConditions",
"MultiFileFlag": "SingleFile"
},
"nodal_results" : []
}
}
""")
)
gid_output.ExecuteInitialize()
gid_output.ExecuteBeforeSolutionLoop()
gid_output.ExecuteInitializeSolutionStep()
gid_output.PrintOutput()
gid_output.ExecuteFinalizeSolutionStep()
gid_output.ExecuteFinalize() 
As said before, the re-meshing is based in a process structure, in this case the 'MainKratos.py' files must be modified (you can take as reference one present in the next section). The parameters that define this process are the following ones:
## Settings string in json format
default_parameters = KratosMultiphysics.Parameters("""
{
"mesh_id" : 0,
"filename" : "out",
"model_part_name" : "MainModelPart",
"strategy" : "LevelSet",
"level_set_strategy_parameters" :{
"scalar_variable" : "DISTANCE",
"gradient_variable" : "DISTANCE_GRADIENT"
},
"error_strategy_parameters" :{
"compute_error_extra_parameters":
{
"stress_vector_variable" : "CAUCHY_STRESS_VECTOR"
},
"error_metric_parameters" :
{
"error_threshold" : 0.05,
"interpolation_error" : 0.04
},
"set_target_number_of_elements" : false,
"target_number_of_elements" : 1000,
"perform_nodal_h_averaging" : false,
"max_iterations" : 3
},
"framework" : "Eulerian",
"internal_variables_parameters" :
{
"allocation_size" : 1000,
"bucket_size" : 4,
"search_factor" : 2,
"interpolation_type" : "LST",
"internal_variable_interpolation_list" :[]
},
"hessian_strategy_parameters" :{
"metric_variable" : ["DISTANCE"],
"estimate_interpolation_error" : false,
"interpolation_error" : 0.04,
"mesh_dependent_constant" : 0.28125
},
"enforce_current" : true,
"initial_step" : 1,
"step_frequency" : 0,
"automatic_remesh" : true,
"automatic_remesh_parameters" :{
"automatic_remesh_type" : "Ratio",
"min_size_ratio" : 1.0,
"max_size_ratio" : 3.0,
"refer_type" : "Mean",
"min_size_current_percentage" : 50.0,
"max_size_current_percentage" : 98.0
},
"initial_remeshing" : false,
"fix_contour_model_parts" : [],
"fix_conditions_model_parts" : [],
"fix_elements_model_parts" : [],
"force_min" : false,
"minimal_size" : 0.1,
"force_max" : false,
"maximal_size" : 10.0,
"advanced_parameters" :
{
"force_hausdorff_value" : false,
"hausdorff_value" : 0.0001,
"no_move_mesh" : false,
"no_surf_mesh" : false,
"no_insert_mesh" : false,
"no_swap_mesh" : false,
"deactivate_detect_angle" : false,
"force_gradation_value" : false,
"gradation_value" : 1.3
},
"anisotropy_remeshing" : true,
"anisotropy_parameters":{
"reference_variable_name" : "DISTANCE",
"hmin_over_hmax_anisotropic_ratio" : 0.01,
"boundary_layer_max_distance" : 1.0,
"boundary_layer_min_size_ratio" : 2.0,
"interpolation" : "Linear"
},
"save_external_files" : false,
"max_number_of_searchs" : 1000,
"interpolate_non_historical" : true,
"extrapolate_contour_values" : true,
"search_parameters" : {
"allocation_size" : 1000,
"bucket_size" : 4,
"search_factor" : 2.0
},
"debug_mode" : false,
"debug_result_mesh" : false,
"initialize_entities" : true,
"echo_level" : 3
}
""")The meaning of each of the parameters is the following one:
-
output_file_name: This is the name of*.soland*.meshgenerated in the case you chose to activatesave_external_files. -
model_part_name: This is important, it should correspond with the name of your actual main model part. -
strategy: The type of strategy to chose, orLevelSetorHessian. -
If you chose the
LevelSetstrategy:-
scalar_variable:The scalar variable used to calculate the gradient and remesh. -
gradient_variable: The variable where this gradient will be stored.
-
-
If you chose the
Hessianstrategy:-
metric_variable: The list of variables that can be considered to calculate the metrics of re-meshing. -
interpolation_error: The interpolation error considered in the re-mesh. -
mesh_dependent_constant: This value is automatically calculated if set to 0, but many definitions can be found in the literature.
-
-
framework: Whatever you want to work "fluids" usingEulerianor "solids" usingLagrangian. If you chooseLagrangianyou will need to interpolate the internal variables if you are considering any constitutive model with history (damage or plasticity).-
bucket_size: The size of the bucket used in the tree search. -
allocation_size: The maximum size to allocate the GP used in the search. -
search_factor: The factor that will be used to search near GP, will take the radius of the current element and multiply by this factor. -
internal_variable_interpolation_list: The list containing the internal variables that will be interpolated. -
interpolation_type: There are mainly two ways to interpolate the internal variables (there are three, but just two are behave correctly): *CPT: Closest point transfer. It transfer the values from the closest GP *LST: Least-square projection transfer. It transfers from the closest GP from the old mesh *SFT: It transfer GP values to the nodes in the old mesh and then interpolate to the new mesh using the shape functions all the time (NOTE: THIS DOESN'T WORK PROPERLY, AND REQUIRES EXTRA STORE)
-
-
enforce_current: If the current size will be enforce as minimum. -
initial_step: The first step to consider to count for the re-meshing. -
step_frequency: The re-mesh will be performed each this number of steps. -
automatic_remesh: If to re-mesh according ratios or manually.-
automatic_remesh_type: If the automatic re-meshed is performed according a ratio or statistically -
min_size_ratio: The proportional ratio of the minimum respect the mean or medianNODAL_H -
max_size_ratio: The proportional ratio of the maximum respect the mean or medianNODAL_H -
refer_type: This can be chosen between the mean or the median, the mean is the default value. -
min_size_current_percentage: When the minimum size is defined statistically, this is the minimum size percentile -
max_size_current_percentage: When the maximum size is defined statistically, this is the maximum size percentile
-
-
advanced_parameters: These are advanced MMG parameters-
force_hausdorff_value: If the Hausdorff is set. This parameter controls the smoothness of the contour -
hausdorff_value: Global Hausdorff value (default value = 0.01) applied on the whole boundary -
no_move_mesh: Avoid/allow point relocation -
no_surf_mesh: Avoid/allow surface modifications -
no_insert_mesh: Don't insert nodes on mesh -
no_swap_mesh: Don't swap mesh -
deactivate_detect_angle: Set the angle detection as activated -
force_gradation_value: If the gradation of the mesh will be enforced -
gradation_value: Set the gradation
-
-
initial_remeshing: If to perform some remeshing in the initialization process -
fix_contour_model_parts: This is a list with the submodelparts of the contour where you desire to fix the nodes. -
fix_conditions_model_parts: The same, but applied for conditions -
fix_elements_model_parts: Idem, but in this case for elements -
minimal_size: When the minimum size is specified manually -
maximal_size: When the maximum size is specified manually -
anisotropy_remeshing: If the anisotropy should be considered in the computation of the remeshing-
hmin_over_hmax_anisotropic_ratio: The minimal anisotropic ratio considered (NOTE: 0 is the maximum value of anisotropy, 1 is not anisotropic at all) -
boundary_layer_max_distance: When the threshold value is specified manually -
boundary_layer_min_size_ratio: When the threshold value is specified using a ratio of reference -
interpolation: The interpolation algorithm used in the anisotropic area. By default is linear, which means that is increasing until the value to the reference is zero.
-
-
save_external_files: This activates the saving of the resulting meshes (in*.meshand*.solfiles) -
max_number_of_searchs: This is the max. number of search that can be done in the value interpolation process (when values are interpolated from the old mesh to the new mesh) -
debug_mode: If true will output a GiD file with just after each remesh (could be useful to check if the error is in the generated mesh). -
echo_level: This sets theecho_level, 0 for no output at all, 3 for standard output.
Can you show us a little example?
Of course, in the examples repository you can find some examples using the process that you can run in your machine.
This problem consists in a 2D fluid problem with continuous re-meshing using the Hessian of the velocity as reference. The resulting output should look something similar to the this.

The same case in 3D. The resulting output should look something similar to the this.

The problems presented in the tests can be used as reference too.
- Getting Kratos (Last compiled Release)
- Compiling Kratos
- Running an example from GiD
- Kratos input files and I/O
- Data management
- Solving strategies
- Manipulating solution values
- Multiphysics
- Video tutorials
- Style Guide
- Authorship of Kratos files
- Configure .gitignore
- How to configure clang-format
- How to use smart pointer in Kratos
- How to define adjoint elements and response functions
- Visibility and Exposure
- Namespaces and Static Classes
Kratos structure
Conventions
Solvers
Debugging, profiling and testing
- Compiling Kratos in debug mode
- Debugging Kratos using GDB
- Cross-debugging Kratos under Windows
- Debugging Kratos C++ under Windows
- Checking memory usage with Valgind
- Profiling Kratos with MAQAO
- Creating unitary tests
- Using ThreadSanitizer to detect OMP data race bugs
- Debugging Memory with ASAN
HOW TOs
- How to create applications
- Python Tutorials
- Kratos For Dummies (I)
- List of classes and variables accessible via python
- How to use Logger
- How to Create a New Application using cmake
- How to write a JSON configuration file
- How to Access DataBase
- How to use quaternions in Kratos
- How to do Mapping between nonmatching meshes
- How to use Clang-Tidy to automatically correct code
- How to use the Constitutive Law class
- How to use Serialization
- How to use GlobalPointerCommunicator
- How to use PointerMapCommunicator
- How to use the Geometry
- How to use processes for BCs
- How to use Parallel Utilities in futureproofing the code
- Porting to Pybind11 (LEGACY CODE)
- Porting to AMatrix
- How to use Cotire
- Applications: Python-modules
- How to run multiple cases using PyCOMPSs
- How to apply a function to a list of variables
- How to use Kratos Native sparse linear algebra
Utilities
Kratos API
Kratos Structural Mechanics API