My aim was just simulating the LFSR logic with flip-flops. So, i didn't use any operator other than ^ (XOR) operator. I am using a basic array to represent flip-flops. After clock tick we are pop out the last element from array and adding new bit to that array.
In real we don't need array. Actually we shouldn't use. We are using bitwise operator to shifting bits. That's why bitwise are there.
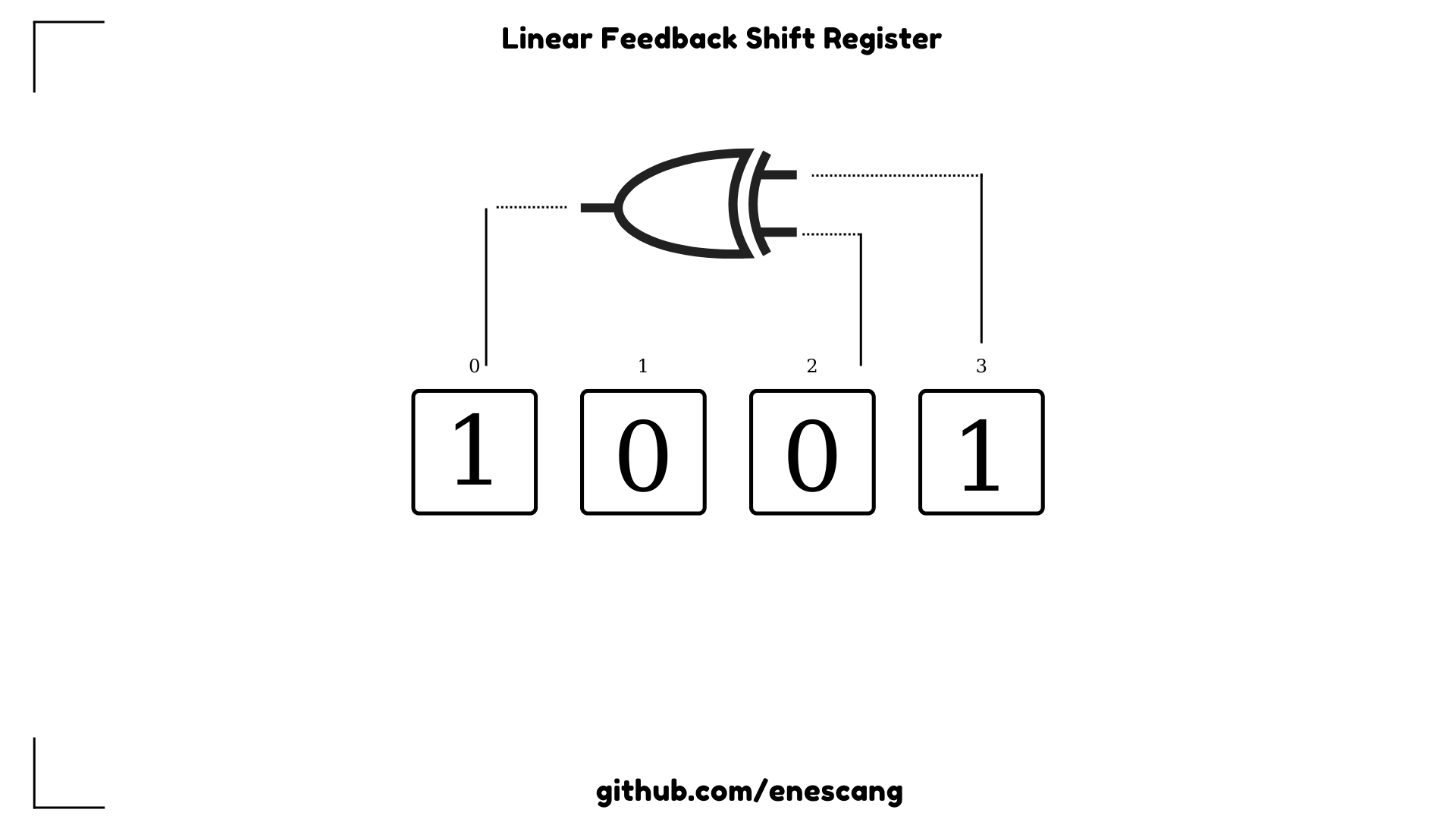
"(LFSR) is a shift register whose input bit is a linear function of its previous state." And XOR is a most commonly used linear function in LFSR. In theory we have several flip-flops and as known as every flip-flop has 1 bit. In every clock tick we are shifting whole bits. Then calculating the new bit based on some math function. Generally irreducible polynomials are using.
There are different types of implementation. In this repo i am using Many-to-One type.
Flip-flops: [1, 0, 1, 1, 1, 0, 1, 1] Taps: [1, 2, 3, 7]
| (index) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 221 | 238 | 119 | 59 | 157 | 78 | 167 | 83 | 169 | 84 |
- Seed Flip-flops and set taps
- Calculate new bit using XOR
- Pop-out the last element from array
- Add the new bit to beginning of array
| F1 | F2 | XOR |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
There are many applications of LFSR. I think LFSR is a great approach to create pseduo numbers. In this example i tried to simulate how LFSR works.
Written with StackEdit.