1.Swin-Transformer作为Faster—RCNN和YOLOV3的backbone,作为特征提取的主干网络,在一定程度上替换了传统卷积神经网络Resnet和DarkNet等这些backbone作为的特征提取网络。
自从Transformer[1]在NLP任务上取得突破性的进展之后,业内一直尝试着把Transformer用于在CV领域。之前的若干尝试,例如iGPT[2],ViT[3]都是将Transformer用在了图像分类领域,目前这些方法都有两个非常严峻的问题
- 受限于图像的矩阵性质,一个能表达信息的图片往往至少需要几百个像素点,而建模这种几百个长序列的数据恰恰是Transformer的天生缺陷;
- 目前的基于Transformer框架更多的是用来进行图像分类,理论上来讲解决检测问题应该也比较容易,但是对实例分割这种密集预测的场景Transformer并不擅长解决。
本文提出的Swin Transformer [4]解决了这两个问题,并且在分类,检测,分割任务上都取得了SOTA的效果。Swin Transformer的最大贡献是提出了一个可以广泛应用到所有计算机视觉领域的backbone,并且大多数在CNN网络中常见的超参数在Swin Transformer中也是可以人工调整的,例如可以调整的网络块数,每一块的层数,输入图像的大小等等。该网络架构的设计非常巧妙,是一个非常精彩的将Transformer应用到图像领域的结构,值得每个AI领域的人前去学习。
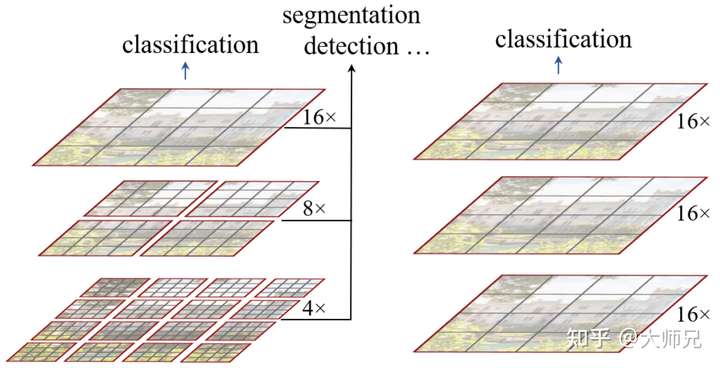
在Swin Transformer之前的ViT和iGPT,它们都使用了小尺寸的图像作为输入,这种直接resize的策略无疑会损失很多信息。与它们不同的是,Swin Transformer的输入是图像的原始尺寸,例如ImageNet的224*224。另外Swin Transformer使用的是CNN中最常用的层次的网络结构,在CNN中一个特别重要的一点是随着网络层次的加深,节点的感受野也在不断扩大,这个特征在Swin Transformer中也是满足的。Swin Transformer的这种层次结构,也赋予了它可以像FPN[6],U-Net[7]等结构实现可以进行分割或者检测的任务。Swin Transformer和ViT的对比如图1。
本文将结合它的pytorch源码对这篇论文的算法细节以及代码实现展开详细介绍,并对论文中解释模糊的地方具体分析。读完此文,你将完全了解清楚Swin Transfomer的结构细节以及设计动机,现在我们开始吧。
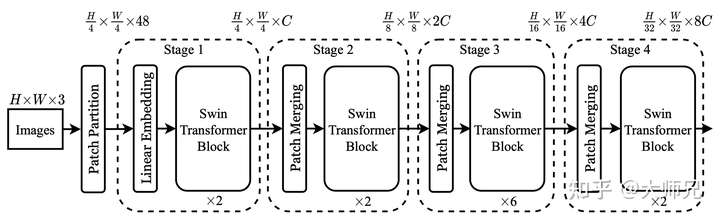
Swin Transformer共提出了4个网络框架,它们从小到大依次是Swin-T,Swin-S, Swin-B和Swin-L,为了绘图简单,本文以最简单的Swin-T作为示例来讲解,Swin-T的结构如图2所示。Swin Transformer最核心的部分便是4个Stage中的Swin Transformer Block,它的具体在如图3所示。
class SwinTransformer(nn.Module):
def __init__(self, *, hidden_dim, layers, heads, channels=3, num_classes=1000, head_dim=32, window_size=7, downscaling_factors=(4, 2, 2, 2), relative_pos_embedding=True):
super().__init__()
self.stage1 = StageModule(in_channels=channels, hidden_dimension=hidden_dim, layers=layers[0], downscaling_factor=downscaling_factors[0], num_heads=heads[0], head_dim=head_dim, window_size=window_size, relative_pos_embedding=relative_pos_embedding)
self.stage2 = StageModule(in_channels=hidden_dim, hidden_dimension=hidden_dim * 2, layers=layers[1], downscaling_factor=downscaling_factors[1], num_heads=heads[1], head_dim=head_dim, window_size=window_size, relative_pos_embedding=relative_pos_embedding)
self.stage3 = StageModule(in_channels=hidden_dim * 2, hidden_dimension=hidden_dim * 4, layers=layers[2], downscaling_factor=downscaling_factors[2], num_heads=heads[2], head_dim=head_dim, window_size=window_size, relative_pos_embedding=relative_pos_embedding)
self.stage4 = StageModule(in_channels=hidden_dim * 4, hidden_dimension=hidden_dim * 8, layers=layers[3], downscaling_factor=downscaling_factors[3], num_heads=heads[3], head_dim=head_dim, window_size=window_size, relative_pos_embedding=relative_pos_embedding)
self.mlp_head = nn.Sequential(
nn.LayerNorm(hidden_dim * 8),
nn.Linear(hidden_dim * 8, num_classes)
)
def forward(self, img):
x = self.stage1(img)
x = self.stage2(x)
x = self.stage3(x)
x = self.stage4(x) # (1, 768, 7, 7)
x = x.mean(dim=[2, 3]) # (1,768)
return self.mlp_head(x)从源码中我们可以看出Swin Transformer的网络结构非常简单,由4个stage和一个输出头组成,非常容易扩展。Swin Transformer的4个Stage的网络框架的是一样的,每个Stage仅有几个基本的超参来调整,包括隐层节点个数,网络层数,多头自注意的头数,降采样的尺度等,这些超参的在源码的具体值如下面片段,本文也会以这组参数对网络结构进行详细讲解。
net = SwinTransformer(
hidden_dim=96,
layers=(2, 2, 6, 2),
heads=(3, 6, 12, 24),
channels=3,
num_classes=3,
head_dim=32,
window_size=7,
downscaling_factors=(4, 2, 2, 2),
relative_pos_embedding=True
)在图2中,输入图像之后是一个Patch Partition,再之后是一个Linear Embedding层,这两个加在一起其实就是一个Patch Merging层(至少上面的源码中是这么实现的)。这一部分的源码如下:
class PatchMerging(nn.Module):
def __init__(self, in_channels, out_channels, downscaling_factor):
super().__init__()
self.downscaling_factor = downscaling_factor
self.patch_merge = nn.Unfold(kernel_size=downscaling_factor, stride=downscaling_factor, padding=0)
self.linear = nn.Linear(in_channels * downscaling_factor ** 2, out_channels)
def forward(self, x):
b, c, h, w = x.shape
new_h, new_w = h // self.downscaling_factor, w // self.downscaling_factor
x = self.patch_merge(x) # (1, 48, 3136)
x = x.view(b, -1, new_h, new_w).permute(0, 2, 3, 1) # (1, 56, 56, 48)
x = self.linear(x) # (1, 56, 56, 96)
return xPatch Merging的作用是对图像进行降采样,类似于CNN中Pooling层。Patch Merging是主要是通过nn.Unfold函数实现降采样的,nn.Unfold的功能是对图像进行滑窗,相当于卷积操作的第一步,因此它的参数包括窗口的大小和滑窗的步长。根据源码中给出的超参我们知道这一步降采样的比例是 ,因此经过
nn.Unfold之后会得到 个长度为
的特征向量,其中
是输入到这个stage的Feature Map的通道数,第一个stage的输入是RGB图像,因此通道数为3,表示为式(1)。
接着的view和permute是将得到的向量序列还原到 的二维矩阵,
linear是将长度是 的特征向量映射到
out_channels的长度,因此stage-1的Patch Merging的输出向量维度是 ,对比源码的注释,这里省略了第一个batch为
的维度。
可以看出Patch Partition/Patch Merging起到的作用像是CNN中通过带有步长的滑窗来降低分辨率,再通过 卷积来调整通道数。不同的是在CNN中最常使用的降采样的最大池化或者平均池化往往会丢弃一些信息,例如最大池化会丢弃一个窗口内的地响应值,而Patch Merging的策略并不会丢弃其它响应,但它的缺点是带来运算量的增加。在一些需要提升模型容量的场景中,我们其实可以考虑使用Patch Merging来替代CNN中的池化。
如我们上面分析的,图2中的Patch Partition+Linaer Embedding就是一个Patch Marging,因此Swin Transformer的一个stage便可以看做由Patch Merging和Swin Transformer Block组成,源码如下。
class StageModule(nn.Module):
def __init__(self, in_channels, hidden_dimension, layers, downscaling_factor, num_heads, head_dim, window_size,
relative_pos_embedding):
super().__init__()
assert layers % 2 == 0, 'Stage layers need to be divisible by 2 for regular and shifted block.'
self.patch_partition = PatchMerging(in_channels=in_channels, out_channels=hidden_dimension,
downscaling_factor=downscaling_factor)
self.layers = nn.ModuleList([])
for _ in range(layers // 2):
self.layers.append(nn.ModuleList([
SwinBlock(dim=hidden_dimension, heads=num_heads, head_dim=head_dim, mlp_dim=hidden_dimension * 4,
shifted=False, window_size=window_size, relative_pos_embedding=relative_pos_embedding),
SwinBlock(dim=hidden_dimension, heads=num_heads, head_dim=head_dim, mlp_dim=hidden_dimension * 4,
shifted=True, window_size=window_size, relative_pos_embedding=relative_pos_embedding),
]))
def forward(self, x):
x = self.patch_partition(x)
for regular_block, shifted_block in self.layers:
x = regular_block(x)
x = shifted_block(x)
return x.permute(0, 3, 1, 2)Swin Transformer Block是该算法的核心点,它由窗口多头自注意层(window multi-head self-attention, W-MSA)和移位窗口多头自注意层(shifted-window multi-head self-attention, SW-MSA)组成,如图3所示。由于这个原因,Swin Transformer的层数要为2的整数倍,一层提供给W-MSA,一层提供给SW-MSA。
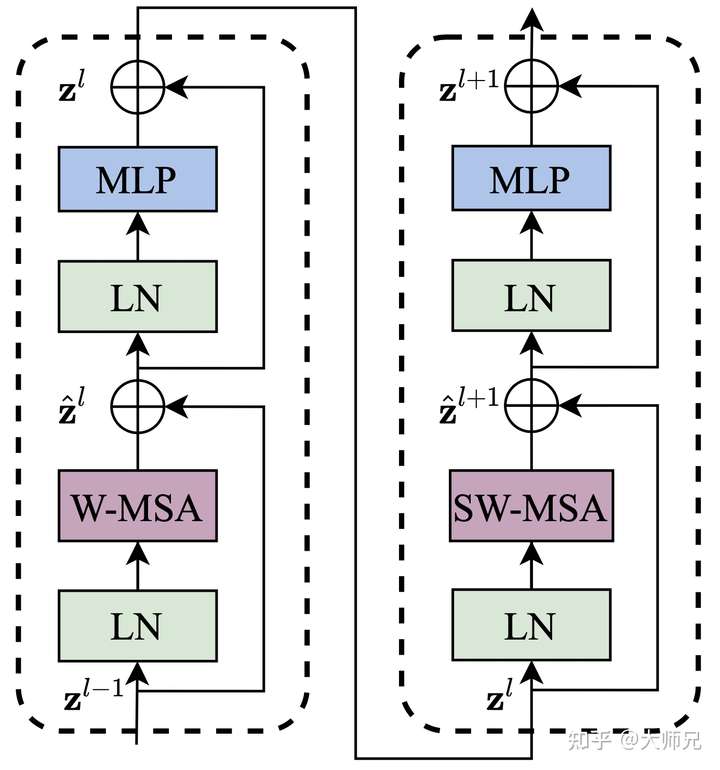
从图3中我们可以看出输入到该stage的特征 先经过LN进行归一化,再经过W-MSA进行特征的学习,接着的是一个残差操作得到
。接着是一个LN,一个MLP以及一个残差,得到这一层的输出特征
。SW-MSA层的结构和W-MSA层类似,不同的是计算特征部分分别使用了SW-MSA和W-MSA,可以从上面的源码中看出它们除了
shifted的这个bool值不同之外,其它的值是保持完全一致的。这一部分可以表示为式(2)。
一个Swin Block的源码如下所示,和论文中图不同的是,LN层(PerNorm函数)从Self-Attention之前移到了Self-Attention之后。
class Residual(nn.Module):
def __init__(self, fn):
super().__init__()
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(x, **kwargs) + x
class PreNorm(nn.Module):
def __init__(self, dim, fn):
super().__init__()
self.norm = nn.LayerNorm(dim)
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(self.norm(x), **kwargs)
class SwinBlock(nn.Module):
def __init__(self, dim, heads, head_dim, mlp_dim, shifted, window_size, relative_pos_embedding):
super().__init__()
self.attention_block = Residual(PreNorm(dim, WindowAttention(dim=dim, heads=heads, head_dim=head_dim, shifted=shifted, window_size=window_size, relative_pos_embedding=relative_pos_embedding)))
self.mlp_block = Residual(PreNorm(dim, FeedForward(dim=dim, hidden_dim=mlp_dim)))
def forward(self, x):
x = self.attention_block(x)
x = self.mlp_block(x)
return x窗口多头自注意力(Window Multi-head Self Attention,W-MSA),顾名思义,就是个在窗口的尺寸上进行Self-Attention计算,与SW-MSA不同的是,它不会进行窗口移位,它们的源码如下。我们这里先忽略shifted为True的情况,这一部分会放在1.6节去讲。
class WindowAttention(nn.Module):
def __init__(self, dim, heads, head_dim, shifted, window_size, relative_pos_embedding):
super().__init__()
inner_dim = head_dim * heads
self.heads = heads
self.scale = head_dim ** -0.5
self.window_size = window_size
self.relative_pos_embedding = relative_pos_embedding # (13, 13)
self.shifted = shifted
if self.shifted:
displacement = window_size // 2
self.cyclic_shift = CyclicShift(-displacement)
self.cyclic_back_shift = CyclicShift(displacement)
self.upper_lower_mask = nn.Parameter(create_mask(window_size=window_size, displacement=displacement, upper_lower=True, left_right=False), requires_grad=False) # (49, 49)
self.left_right_mask = nn.Parameter(create_mask(window_size=window_size, displacement=displacement,pper_lower=False, left_right=True), requires_grad=False) # (49, 49)
self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False)
if self.relative_pos_embedding:
self.relative_indices = get_relative_distances(window_size) + window_size - 1
self.pos_embedding = nn.Parameter(torch.randn(2 * window_size - 1, 2 * window_size - 1))
else:
self.pos_embedding = nn.Parameter(torch.randn(window_size ** 2, window_size ** 2))
self.to_out = nn.Linear(inner_dim, dim)
def forward(self, x):
if self.shifted:
x = self.cyclic_shift(x)
b, n_h, n_w, _, h = *x.shape, self.heads # [1, 56, 56, _, 3]
qkv = self.to_qkv(x).chunk(3, dim=-1) # [(1,56,56,96), (1,56,56,96), (1,56,56,96)]
nw_h = n_h // self.window_size # 8
nw_w = n_w // self.window_size # 8
# 分成 h/M * w/M 个窗口
q, k, v = map( lambda t: rearrange(t, 'b (nw_h w_h) (nw_w w_w) (h d) -> b h (nw_h nw_w) (w_h w_w) d', h=h, w_h=self.window_size, w_w=self.window_size), qkv)
# q, k, v : (1, 3, 64, 49, 32)
# 按窗口个数的self-attention
dots = einsum('b h w i d, b h w j d -> b h w i j', q, k) * self.scale # (1,3,64,49,49)
if self.relative_pos_embedding:
dots += self.pos_embedding[self.relative_indices[:, :, 0], self.relative_indices[:, :, 1]]
else:
dots += self.pos_embedding
if self.shifted:
dots[:, :, -nw_w:] += self.upper_lower_mask
dots[:, :, nw_w - 1::nw_w] += self.left_right_mask
attn = dots.softmax(dim=-1) # (1,3,64,49,49)
out = einsum('b h w i j, b h w j d -> b h w i d', attn, v)
out = rearrange(out, 'b h (nw_h nw_w) (w_h w_w) d -> b (nw_h w_h) (nw_w w_w) (h d)', h=h, w_h=self.window_size, w_w=self.window_size, nw_h=nw_h, nw_w=nw_w) # (1, 56, 56, 96) # 窗口合并
out = self.to_out(out)
if self.shifted:
out = self.cyclic_back_shift(out)
return out在forward函数中首先计算的是Transformer中介绍的 ,
,
三个特征。所以
to_qkv()函数就是一个线性变换,这里使用了一个实现小技巧,即只使用了一个一层隐层节点数为inner_dim*3的线性变换,然后再使用chunk(3)操作将它们切开。因此qkv是一个长度为3的Tensor,每个Tensor的维度是 。
之后的map函数是实现W-MSA中的W最核心的代码,它是通过einops的rearrange实现的。einops是一个可读性非常高的实现常见矩阵操作的python包,例如矩阵转置,矩阵复制,矩阵reshape等操作。最终通过这个操作得到了3个独立的窗口的权值矩阵,它们的维度是 ,这4个值的意思分别是:
Swin Transformer将计算区域控制在了以窗口为单位的策略极大减轻了网络的计算量,将复杂度降低到了图像尺寸的线性比例。传统的MSA和W-MSA的复杂度分别是:
(3)式的计算忽略了softmax的占用的计算量,这里以 为例,它的具体构成如下:
- 代码中的
to_qkv()函数,即用于生成三个特征向量:其中
。
的维度是
,
的维度是
,那么这三项的复杂度是
;
- 计算
:
的维度均是
,因此它的复杂度是
;
- softmax之后乘
得到
:因为
的维度是
,所以它的复杂度是
;
乘
矩阵得到最终输出,对应代码中的
to_out()函数:它的复杂度是。
通过Transformer的计算公式(4),我们可以有更直观一点的理解,在Transformer一文中我们介绍过Self-Attention是通过点乘的方式得到Query矩阵和Key矩阵的相似度,即(4)式中的 。然后再通过这个相似度匹配Value。因此这个相似度的计算时通过逐个元素进行点乘计算得到的。如果比较的范围是一个图像,那么计算的瓶颈就是整个图的逐像素比较,因此复杂度是
。而W-MSA是在窗口内的逐像素比较,因此复杂度是
,其中
是W-MSA的窗口的大小。
回到代码,接着的dots变量便是我们刚刚介绍的 操作。接着是加入相对位置编码,我们放到最后介绍。接着的
attn以及einsum便是完成了式(4)的整个流程。然后再次使用rearrange将维度再调整回 。最后通过
to_out将维度调整为超参设置的输出维度的值。
这里我们介绍一下W-MSA的相对位置编码,首先这个位置编码是加在乘以完归一化尺度之后的dots变量上的,因此 的计算方式变为式(5)。因为W-MSA是以窗口为单位进行特征匹配的,因此相对位置编码的范围也应该是以窗口为单位,它的具体实现见下面代码。相对位置编码的具体思想参考UniLMv2[8]。
def get_relative_distances(window_size):
indices = torch.tensor(np.array([[x, y] for x in range(window_size) for y in range(window_size)]))
distances = indices[None, :, :] - indices[:, None, :]
return distances单独的使用W-MSA得到的网络的建模能力是非常差的,因为它将每个窗口当做一个独立区域计算而忽略了窗口之间交互的必要性,基于这个动机,Swin Transformer提出了SW-MSA。
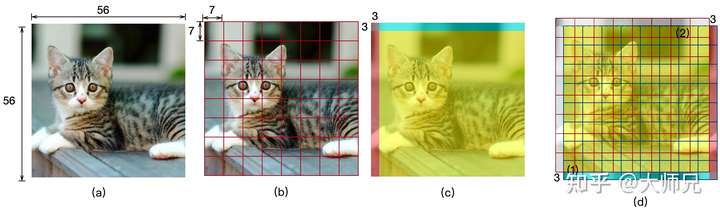
SW-MSA的的位置是接在W-MSA层之后的,因此只要我们提供一种和W-MSA不同的窗口切分方式便可以实现跨窗口的通信。SW-MSA的实现方式如图4所示。我们上面说过,输入到Stage-1的图像尺寸是 的(图4.(a)),那么W-MSA的窗口切分的结果如图4.(b)所示。那么我们如何得到和W-MSA不同的切分方式呢?SW-MSA的思想很简单,将图像各循环上移和循环左移半个窗口的大小,那么图4.(c)的蓝色和红色区域将分别被移动到图像的下侧和右侧,如图4.(d)。那么在移位的基础上再按照W-MSA切分窗口,就会得到和W-MSA不同的窗口切分方式,如图4.(d)中红色和蓝色分别是W-MSA和SW-MSA的切分窗口的结果。这一部分可以通过pytorch的
roll函数实现,源码中是CyclicShift函数。
class CyclicShift(nn.Module):
def __init__(self, displacement):
super().__init__()
self.displacement = displacement
def forward(self, x):
return torch.roll(x, shifts=(self.displacement, self.displacement), dims=(1, 2))其中displacement的值是窗口值除2。
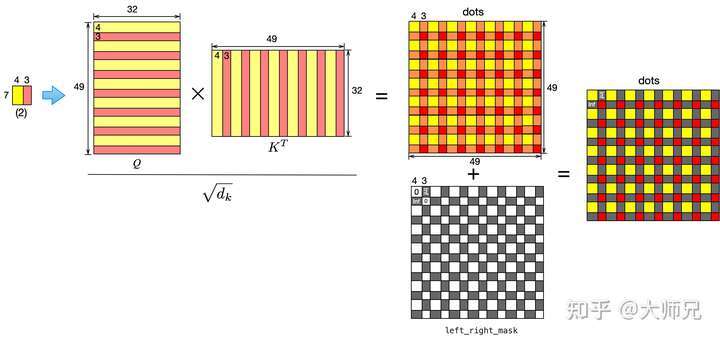
这种窗口切分方式引入了一个新的问题,即在移位图像的最后一行和最后一列各引入了一块移位过来的区域,如图4.(d)。根据上面我们介绍的 用于逐像素计算相似度的自注意力机制,图像两侧的像素互相计算相似度是没有任何作用的,即只需要对比图4.(d)中的一个窗口中相同颜色的区域,我们以图4.(d)左下角的区域(1)为例来说明SW-MSA是怎么实现这个功能的。
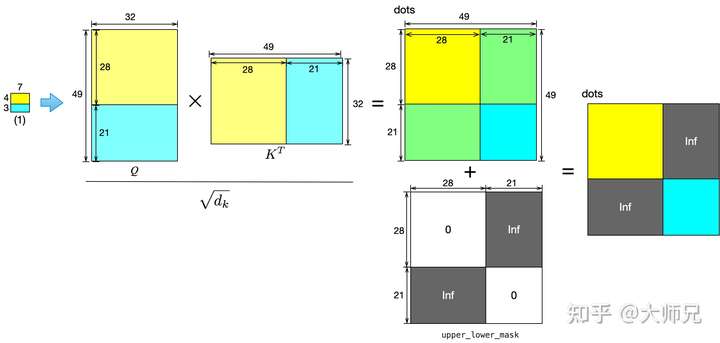
区域(1)的计算如图5所示。首先一个 大小的窗口通过线性预算得到
,
,
三个权值,如我们介绍的,它的维度是
。在这个49中,前28个是按照滑窗的方式遍历区域(1)中的前48个像素得到的,后21个则是遍历区域(1)的下半部分得到的,此时他们对应的位置关系依旧保持上黄下蓝的性质。
接着便是计算 ,在图中相同颜色区域的相互计算后会依旧保持颜色,而黄色和蓝色区域计算后会变成绿色,而绿色的部分便是无意义的相似度。在论文中使用了
upper_lower_mask将其掩码掉,upper_lower_mask是由 和无穷大组成的二值矩阵,最后通过单位加之后得到最终的
dots变量。
upper_lower_mask的计算方式如下。
mask = torch.zeros(window_size ** 2, window_size ** 2)
mask[-displacement * window_size:, :-displacement * window_size] = float('-inf')
mask[:-displacement * window_size, -displacement * window_size:] = float('-inf')区域(2)的计算方式和区域(1)类似,不同的是区域(2)是循环左移之后的结果,如图6所示。因为(2)是左右排列的,因此它得到的 ,
,
是条纹状的,即先逐行遍历,在这7行中,都会先遍历到4个黄的,然后再遍历到3个红的。两个条纹状的矩阵相乘后,得到的相似度矩阵是网络状的,其中橙色表示无效区域,因此需要网格状的掩码
left_right_mask来进行覆盖。
left_right_mask的生成方式如下面代码。关于这两个掩码的值,你可以自己代入一些值来验证,你可以设置一下window_size的值,然后displacement的值设为window_size的一半即可。
这一部分操作中,窗口移位和mask的计算是在WindowAttention类中的第一个if shifted = True中实现的。掩码的相加是在第二个if中实现的,最后一个if则是将图像再复原回原来的位置。
mask = torch.zeros(window_size ** 2, window_size ** 2)
mask = rearrange(mask, '(h1 w1) (h2 w2) -> h1 w1 h2 w2', h1=window_size, h2=window_size)
mask[:, -displacement:, :, :-displacement] = float('-inf')
mask[:, :-displacement, :, -displacement:] = float('-inf')
mask = rearrange(mask, 'h1 w1 h2 w2 -> (h1 w1) (h2 w2)')截止到这,我们从头到尾对Swin-T的stage-1进行了完成的梳理,后面3个stage除了几个超参以及图像的尺寸和stage-1不同之外,其它的结构均保持一致,这里不再赘述。
最后我们介绍一下Swin Transformer的输出层,在stage-4完成计算后,特征的维度是 。Swin Transformer先通过一个Global Average Pooling得到长度为768的特征向量,再通过一个LN和一个全连接得到最终的预测结果,如式(6)。
Swin Transformer共提出了4个不同尺寸的模型,它们的区别在于隐层节点的长度,每个stage的层数,多头自注意力机制的头的个数,具体值见下面代码。
def swin_t(hidden_dim=96, layers=(2, 2, 6, 2), heads=(3, 6, 12, 24), **kwargs):
return SwinTransformer(hidden_dim=hidden_dim, layers=layers, heads=heads, **kwargs)
def swin_s(hidden_dim=96, layers=(2, 2, 18, 2), heads=(3, 6, 12, 24), **kwargs):
return SwinTransformer(hidden_dim=hidden_dim, layers=layers, heads=heads, **kwargs)
def swin_b(hidden_dim=128, layers=(2, 2, 18, 2), heads=(4, 8, 16, 32), **kwargs):
return SwinTransformer(hidden_dim=hidden_dim, layers=layers, heads=heads, **kwargs)
def swin_l(hidden_dim=192, layers=(2, 2, 18, 2), heads=(6, 12, 24, 48), **kwargs):
return SwinTransformer(hidden_dim=hidden_dim, layers=layers, heads=heads, **kwargs)因为Swin Transformer是一个多阶段的网络框架,而且每一个阶段的输出也是一组Feature Map,因此可以非常方便的将其迁移到几乎所有CV任务中。作者的实验结果也表明Swin Transformer在检测和分割领域也达到了state-of-the-art的水平。
Swin Transformer是近年来为数不多的读起来让人兴奋的算法,它让人兴奋的点有三:
- 解决了长期困扰业界的Transformer应用到CV领域的速度慢的问题;
- Swin Transformer的设计非常巧妙,具有创新又紧扣CNN的优点,充分考虑的CNN的位移不变性,尺寸不变性,感受野与层次的关系,分阶段降低分辨率增加通道数等特点,没了这些特点Swin Transformer是没有勇气称自己一个backbone的;
- 其在诸多CV领域的STOA的表现。
当然我们对Swin Transformer还是要站在一个客观的角度来评价的,虽然论文中说Swin Transformer是一个backbone,但是这个评价还为时尚早,因为
- Swin Transformer并没有提供一个像反卷积那样的上采样的算法,因此对于这类需求的backbone Swin Transformer并不能直接替换,也许可以采用双线性差值来实现,但效果如何还需要评估。
- 从W-MSA一节中我们可以看出每个窗口都有一组独立的
,
,
,因此Swin Transformer并不具有CNN一个特别重要的特性:权值共享。这也造成了Swin Transformer在速度上和还和同级别的CNN仍有不小的差距。所以就目前来看,在嵌入式平台上CNN还有着不可撼动的地位。
- Swin Transformer在诸多的CNN已经取得非常好的效果的领域还未得到充分验证,如果只会掀起了一股使用Swin Transformer或其衍生算法在CV领域灌水风,那时候我们就可以说:Swin Transformer的时代到来了。
在一定程度上替换了传统卷积神经网络Resnet和DarkNet等这些backbone作为的特征提取网络。DogeNet也是基于Transformer+CNN的特征抽取网络,在图像分类和作为目标检测的backbone都有较好的效果。DogeNet是团队自研网络,源于ResNet(传统残差卷积神经网络)和BotNet(Transformer+CNN),在参数量以及鲁棒性都做了较大改进。而实验结果证明,在参数量减少,网络的特征抽取能力较ResNet和BotNet有较大提升。
| model | Accuracy | R30 | R45 | R60 | R75 | R90 | Channel List | Parameter | FLOPS |
|---|---|---|---|---|---|---|---|---|---|
| res_net26(2x2x2x2) | 95 | 84.4 | 78 | 69.8 | 68.6 | 74 | 64x64x128x256x512 | 14.0M | 2377M |
| res_net50(3x4x6x3) | 95 | 81.8 | 74.4 | 66.4 | 71.6 | 72.4 | 64x64x128x256x512 | 23.5M | 4143M |
| bot_net50_l1(3x4x6x3) | 75.6 | 70.2 | 62.2 | 71.4 | 54.4 | 51.8 | 64x64x128x256x512 | 18.8M | 4094M |
| bot_net50_l2(3x4x6x3) | 75 | N | N | N | N | 52.4 | 64x64x128x256x512 | 14.3M | 3849M |
| doge_net26(2x3x1x2) | 94.2 | 83.2 | 76.2 | 69.2 | 74.6 | 85.4 | 64x32x 48x 96 x128 | 0.9M | 685M |
| doge_net26(2x1x3x2) | 91.4 | 82.4 | 77.6 | 72.8 | 76.2 | 79 | 64x32x 48x 96 x128 | 0.9M | 685M |
| doge_net50(6x6x2x2) | 90.4 | 80.6 | 72.2 | 70.2 | 71 | 77.4 | 64x32x 48x 96 x128 | 1.2M | 1043M |
| dogex26(2x3x1x2) | 88.8 | 77.4 | 72 | 68.6 | 73.4 | 76.2 | 64x32x 48x 96 x128 | 0.83M | 659M |
| dogex50(6x6x2x2) | - | - | - | - | - | - | 64x32x 48x 96 x128 | 1.13M | 1014M |
| shibax26(2x3x1x2)-DSA*2 | 95.8 | 80.8 | 75.8 | 70.2 | 71.2 | 80.4 | 64x32x 48x 96 x128 | 0.82M | 452M |
| shibax50(6x6x2x2)-DSA*2 | 93.8 | 81.8 | 76 | 71.6 | 71.4 | 80.4 | 64x32x 48x 96 x128 | 1.11M | 796M |
| Efficient-net-B0(Origin) | 95.6 | 81.4 | 74.4 | 70.2 | 68.2 | 76.2 | N | 5.3M | 422M |
| Efficient-net-B0(pretrain) | 99.4 | 98.8 | 97.8 | 95 | 92.6 | 94.2 | N | 5.3M | 422M |
| Shiba26(2x3x1x2)-DSA*3 | 93.8 | 81.4 | 77 | 70.8 | 70 | 79.4 | 64x32x 48x 96 x128 | 0.746M | 380M |
| Shiba50(6x6x2x2)-DSA*3 | 92.6 | 81.8 | 74.8 | 68 | 69.2 | 74.6 | 64x32x 48x 96 x128 | 0.938M | 582M |
#定义的deep_sort特征提取器的original_model,dogenet50
import paddle
import paddle.nn as nn
import paddle.nn.functional as F
class BasicBlock(nn.Layer):
def __init__(self, c_in, c_out,is_downsample=False):
super(BasicBlock,self).__init__()
self.is_downsample = is_downsample
if is_downsample:
self.conv1 = nn.Conv2D(c_in, c_out, 3, stride=2, padding=1, bias_attr=False)
else:
self.conv1 = nn.Conv2D(c_in, c_out, 3, stride=1, padding=1, bias_attr=False)
self.bn1 = nn.BatchNorm2D(c_out)
self.relu = nn.ReLU()
self.conv2 = nn.Conv2D(c_out,c_out,3,stride=1,padding=1, bias_attr=False)
self.bn2 = nn.BatchNorm2D(c_out)
if is_downsample:
self.downsample = nn.Sequential(
nn.Conv2D(c_in, c_out, 1, stride=2, bias_attr=False),
nn.BatchNorm2D(c_out)
)
elif c_in != c_out:
self.downsample = nn.Sequential(
nn.Conv2D(c_in, c_out, 1, stride=1, bias_attr=False),
nn.BatchNorm2D(c_out)
)
self.is_downsample = True
def forward(self,x):
y = self.conv1(x)
y = self.bn1(y)
y = self.relu(y)
y = self.conv2(y)
y = self.bn2(y)
if self.is_downsample:
x = self.downsample(x)
return F.relu(x.add(y))
def make_layers(c_in,c_out,repeat_times, is_downsample=False):
blocks = []
for i in range(repeat_times):
if i ==0:
blocks += [BasicBlock(c_in,c_out, is_downsample=is_downsample),]
else:
blocks += [BasicBlock(c_out,c_out),]
return nn.Sequential(*blocks)
class Net(nn.Layer):
def __init__(self, num_classes=625 ,reid=False):
super(Net,self).__init__()
# 3 128 64
self.conv = nn.Sequential(
nn.Conv2D(3,32,3,stride=1,padding=1),
nn.BatchNorm2D(32),
nn.ELU(),
nn.Conv2D(32,32,3,stride=1,padding=1),
nn.BatchNorm2D(32),
nn.ELU(),
nn.MaxPool2D(3,2,padding=1),
)
# 32 64 32
self.layer1 = make_layers(32,32,2,False)
# 32 64 32
self.layer2 = make_layers(32,64,2,True)
# 64 32 16
self.layer3 = make_layers(64,128,2,True)
# 128 16 8
self.dense = nn.Sequential(
nn.Dropout(p=0.6),
nn.Linear(128*16*8, 128),
nn.BatchNorm1D(128),
nn.ELU()
)
# 256 1 1
self.reid = reid
self.batch_norm = nn.BatchNorm1D(128)
self.classifier = nn.Sequential(
nn.Linear(128, num_classes),
)
def forward(self, x):
x = self.conv(x)
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = paddle.reshape(x, [x.shape[0],-1])
if self.reid:
x = self.dense[0](x)
x = self.dense[1](x)
x = paddle.divide(x, paddle.norm(x, p=2, axis=1,keepdim=True))
return x
x = self.dense(x)
# B x 128
# classifier
x = self.classifier(x)
return x2.DogeNet_ReID
import efficientnet_pypaddle
import paddle
import paddle.nn as nn
import paddle.nn.functional as F
from paddle.nn.transformer import models
__all__ = ["get_n_params", "efficient_b0", "res_net50", "bot_net50_l1", "bot_net50_l2", "doge_net26",
"doge_net50", "doge_net_2x1x3x2", "res_net26", "doge_net50_no_embed", "doge_net_2x1x3x2_no_embed",
"doge_net26_no_embed"]
def get_n_params(model):
pp = 0
for p in list(model.parameters()):
nn = 1
for s in list(p.size()):
nn = nn * s
pp += nn
return pp
class SE(nn.Module):
"""Squeeze-and-Excitation block."""
def __init__(self, in_planes, se_planes):
super(SE, self).__init__()
self.se1 = nn.Conv2D(in_planes, se_planes, kernel_size=1, bias=True)
self.se2 = nn.Conv2D(se_planes, in_planes, kernel_size=1, bias=True)
def forward(self, x):
out = F.adaptive_avg_pool2D(x, (1, 1))
out = F.relu(self.se1(out))
out = self.se2(out).sigmoid()
out = x * out
return out
class MHSA(nn.Module):
def __init__(self, n_dims, width=14, height=14, heads=4, position_embedding=True):
super(MHSA, self).__init__()
self.heads = heads
self.position_embedding = position_embedding
self.query = nn.Conv2D(n_dims, n_dims, kernel_size=1)
self.key = nn.Conv2D(n_dims, n_dims, kernel_size=1)
self.value = nn.Conv2D(n_dims, n_dims, kernel_size=1)
if position_embedding:
self.rel_h = nn.Parameter(paddle.randn([1, heads, n_dims // heads, 1, height]), requires_grad=True)
self.rel_w = nn.Parameter(paddle.randn([1, heads, n_dims // heads, width, 1]), requires_grad=True)
self.softmax = nn.Softmax(dim=-1)
def forward(self, x):
n_batch, C, width, height = x.size()
q = self.query(x).view(n_batch, self.heads, C // self.heads, -1)
k = self.key(x).view(n_batch, self.heads, C // self.heads, -1)
v = self.value(x).view(n_batch, self.heads, C // self.heads, -1)
content_content = paddle.matmul(q.permute(0, 1, 3, 2), k)
if self.position_embedding:
content_position = (self.rel_h + self.rel_w).view(1, self.heads, C // self.heads, -1).permute(0, 1, 3, 2)
content_position = paddle.matmul(content_position, q)
energy = content_content + content_position
else:
energy = content_content
attention = self.softmax(energy)
out = paddle.matmul(v, attention.permute(0, 1, 3, 2))
out = out.view(n_batch, C, width, height)
return out
class BottleNeck(nn.Module):
expansion = 4
def __init__(self, in_planes, planes, stride=1, heads=4, mhsa=False, resolution=None):
super(BottleNeck, self).__init__()
self.conv1 = nn.Conv2D(in_planes, planes, kernel_size=1, bias=False)
self.bn1 = nn.BatchNorm2D(planes)
if not mhsa:
self.conv2 = nn.Conv2D(planes, planes, kernel_size=3, padding=1, stride=stride, bias=False)
else:
self.conv2 = nn.ModuleList()
self.conv2.append(MHSA(planes, width=int(resolution[0]), height=int(resolution[1]), heads=heads))
if stride == 2:
self.conv2.append(nn.AvgPool2D(2, 2))
self.conv2 = nn.Sequential(*self.conv2)
self.bn2 = nn.BatchNorm2D(planes)
self.conv3 = nn.Conv2D(planes, self.expansion * planes, kernel_size=1, bias=False)
self.bn3 = nn.BatchNorm2D(self.expansion * planes)
self.shortcut = nn.Sequential()
if stride != 1 or in_planes != self.expansion * planes:
self.shortcut = nn.Sequential(
nn.Conv2D(in_planes, self.expansion * planes, kernel_size=1, stride=stride),
nn.BatchNorm2D(self.expansion * planes)
)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = F.relu(self.bn2(self.conv2(out)))
out = self.bn3(self.conv3(out))
out += self.shortcut(x)
out = F.relu(out)
return out
class DogeNeck(nn.Module):
expansion = 4
def __init__(self, in_planes, planes, stride=1, heads=4, mhsa=False, resolution=None, position_embedding=True):
super(DogeNeck, self).__init__()
self.conv1 = nn.Conv2D(in_planes, planes, kernel_size=1, bias=False)
self.bn1 = nn.BatchNorm2D(planes)
if not mhsa:
self.conv2 = nn.ModuleList()
self.conv2.append(nn.Conv2D(planes, planes, kernel_size=3, padding=1, stride=stride, bias=False))
self.conv2.append(SE(planes, planes // 2))
self.conv2 = nn.Sequential(*self.conv2)
else:
self.conv2 = nn.ModuleList()
self.conv2.append(MHSA(
planes, width=int(resolution[0]), height=int(resolution[1]),
heads=heads, position_embedding=position_embedding
))
if stride == 2:
self.conv2.append(nn.AvgPool2D(2, 2))
self.conv2 = nn.Sequential(*self.conv2)
self.bn2 = nn.BatchNorm2D(planes)
self.conv3 = nn.Conv2D(planes, self.expansion * planes, kernel_size=1, bias=False)
self.bn3 = nn.BatchNorm2D(self.expansion * planes)
self.shortcut = nn.Sequential()
if stride != 1 or in_planes != self.expansion * planes:
self.shortcut = nn.Sequential(
nn.Conv2D(in_planes, self.expansion * planes, kernel_size=1, stride=stride),
nn.BatchNorm2D(self.expansion * planes)
)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = F.relu(self.bn2(self.conv2(out)))
out = self.bn3(self.conv3(out))
out += self.shortcut(x)
out = F.relu(out)
return out
# reference
# /~https://github.com/kuangliu/pypaddle-cifar/blob/master/models/resnet.py
class BotNet(nn.Module):
def __init__(self, block, num_blocks, num_classes=15, resolution=(224, 224), heads=4,
layer3: str = "CNN", in_channel=3):
super(BotNet, self).__init__()
self.in_planes = 64
self.resolution = list(resolution)
self.conv1 = nn.Conv2D(in_channel, 64, kernel_size=7, stride=2, padding=3, bias=False)
if self.conv1.stride[0] == 2:
self.resolution[0] /= 2
if self.conv1.stride[1] == 2:
self.resolution[1] /= 2
self.bn1 = nn.BatchNorm2D(64)
self.relu = nn.ReLU(inplace=True)
self.maxpool = nn.MaxPool2D(kernel_size=3, stride=2, padding=1) # for ImageNet
if self.maxpool.stride == 2:
self.resolution[0] /= 2
self.resolution[1] /= 2
self.layer1 = self._make_layer(block, 64, num_blocks[0], stride=1)
self.layer2 = self._make_layer(block, 128, num_blocks[1], stride=2)
if layer3 == "CNN":
self.layer3 = self._make_layer(block, 256, num_blocks[2], stride=2)
elif layer3 == "Transformer":
self.layer3 = self._make_layer(block, 256, num_blocks[3], stride=2, heads=heads, mhsa=True)
else:
raise NotImplementedError
self.layer4 = self._make_layer(block, 512, num_blocks[3], stride=2, heads=heads, mhsa=True)
self.avgpool = nn.AdaptiveAvgPool2D((1, 1))
self.fc = nn.Sequential(
nn.Dropout(0.3), # All architecture deeper than ResNet-200 dropout_rate: 0.2
nn.Linear(512 * block.expansion, num_classes),
)
def _make_layer(self, block, planes, num_blocks, stride=1, heads=4, mhsa=False):
strides = [stride] + [1] * (num_blocks - 1)
layers = []
for idx, stride in enumerate(strides):
layers.append(block(self.in_planes, planes, stride, heads, mhsa, self.resolution))
if stride == 2:
self.resolution[0] /= 2
self.resolution[1] /= 2
self.in_planes = planes * block.expansion
return nn.Sequential(*layers)
def forward(self, x):
out = self.relu(self.bn1(self.conv1(x)))
out = self.maxpool(out) # for ImageNet
out = self.layer1(out)
out = self.layer2(out)
out = self.layer3(out)
out = self.layer4(out)
out = self.avgpool(out)
out = paddle.flatten(out, 1)
out = self.fc(out)
return out
class DogeNet(nn.Module):
def __init__(self, block, num_blocks, num_classes=15, resolution=(224, 224), heads=4, in_channel=3,
position_embedding=True):
super(DogeNet, self).__init__()
self.in_planes = 64
self.resolution = list(resolution)
self.position_embedding = position_embedding
self.conv1 = nn.Conv2D(in_channel, 64, kernel_size=3, stride=2, padding=1, bias=False)
if self.conv1.stride[0] == 2:
self.resolution[0] /= 2
if self.conv1.stride[1] == 2:
self.resolution[1] /= 2
self.bn1 = nn.BatchNorm2D(64)
self.relu = nn.ReLU(inplace=True)
if self.conv1.stride == 2:
self.resolution[0] /= 2
self.resolution[1] /= 2
self.layer1 = self._make_layer(block, 32, num_blocks[0], stride=2)
self.layer2 = self._make_layer(block, 48, num_blocks[1], stride=2)
self.layer3 = self._make_layer(block, 96, num_blocks[2], stride=2, heads=heads, mhsa=True)
self.layer4 = self._make_layer(block, 128, num_blocks[3], stride=1, heads=heads, mhsa=True)
self.avgpool = nn.AdaptiveAvgPool2D((1, 1))
self.fc = nn.Sequential(
nn.Dropout(0.3),
nn.Linear(128 * block.expansion, num_classes),
)
def _make_layer(self, block, planes, num_blocks, stride=1, heads=4, mhsa=False):
strides = [stride] + [1] * (num_blocks - 1)
layers = []
for idx, stride in enumerate(strides):
layers.append(block(self.in_planes, planes, stride, heads, mhsa, self.resolution, self.position_embedding))
if stride == 2:
self.resolution[0] /= 2
self.resolution[1] /= 2
self.in_planes = planes * block.expansion
return nn.Sequential(*layers)
def forward(self, x):
out = self.relu(self.bn1(self.conv1(x)))
out = self.layer1(out)
out = self.layer2(out)
out = self.layer3(out)
out = self.layer4(out)
out = self.avgpool(out)
out = paddle.flatten(out, 1)
out = self.fc(out)
return out
def efficient_b0(num_classes=10, **kwargs):
return efficientnet_pypaddle.EfficientNet.from_name("efficientnet-b0", num_classes=num_classes)
def res_net50(num_classes=10, **kwargs):
return models.ResNet(models.resnet.Bottleneck, [3, 4, 6, 3], num_classes=num_classes)
def res_net26(num_classes=10, **kwargs):
return models.ResNet(models.resnet.Bottleneck, [2, 2, 2, 2], num_classes=num_classes)
def bot_net50_l1(num_classes=10, args=None, heads=4, **kwargs):
in_shape = args.in_shape
return BotNet(BottleNeck, [3, 4, 6, 3], num_classes=num_classes, # resnet50加入一层transformer
resolution=in_shape[1:], heads=heads, layer3="CNN", in_channel=in_shape[0])
def bot_net50_l2(num_classes=10, args=None, heads=4, **kwargs):
in_shape = args.in_shape
return BotNet(BottleNeck, [3, 4, 6, 3], num_classes=num_classes, # resnet50加入两层transformer
resolution=in_shape[1:], heads=heads, layer3="Transformer", in_channel=in_shape[0])
def doge_net26(num_classes=10, args=None, heads=4, **kwargs):
in_shape = args.in_shape
return DogeNet(DogeNeck, [2, 3, 1, 2], num_classes=num_classes,
resolution=in_shape[1:], heads=heads, in_channel=in_shape[0])
def doge_net50(num_classes=4, args=None, heads=4, **kwargs):
in_shape = (3, 224, 224)
return DogeNet(DogeNeck, [6, 6, 2, 2], num_classes=num_classes,
resolution=in_shape[1:], heads=heads, in_channel=in_shape[0])
def doge_net_2x1x3x2(num_classes=10, args=None, heads=4, **kwargs):
in_shape = args.in_shape
return DogeNet(DogeNeck, [2, 3, 1, 2], num_classes=num_classes,
resolution=in_shape[1:], heads=heads, in_channel=in_shape[0])
def doge_net26_no_embed(num_classes=10, args=None, heads=4, **kwargs):
in_shape = args.in_shape
return DogeNet(DogeNeck, [2, 3, 1, 2], num_classes=num_classes,
resolution=in_shape[1:], heads=heads, in_channel=in_shape[0], position_embedding=False)
def doge_net50_no_embed(num_classes=10, args=None, heads=4, **kwargs):
in_shape = args.in_shape
return DogeNet(DogeNeck, [6, 6, 2, 2], num_classes=num_classes,
resolution=in_shape[1:], heads=heads, in_channel=in_shape[0], position_embedding=False)
def doge_net_2x1x3x2_no_embed(num_classes=10, args=None, heads=4, **kwargs):
in_shape = args.in_shape
return DogeNet(DogeNeck, [2, 3, 1, 2], num_classes=num_classes,
resolution=in_shape[1:], heads=heads, in_channel=in_shape[0], position_embedding=False)
if __name__ == '__main__':
from paddlesummary import summary
from core.utils.argparse import arg_parse
args = arg_parse().parse_args()
args.in_shape = (3, 224, 224)
x = paddle.randn([1, 3, 224, 224])
model = doge_net26(args=args, heads=4) # 904994
# model = doge_net50_64x64(resolution=tuple(x.shape[2:]), heads=8) # 4178255
# model = efficient_b0()
# model = efficientnet_pypaddle.EfficientNet.from_name("efficientnet-b0")
print(model(x).size())
print(get_n_params(model))
# 打印网络结构
summary(model, input_size=[(3, 224, 224)], batch_size=1, device="cpu")[1] Vaswani, Ashish, et al. "Attention is all you need." arXiv preprint arXiv:1706.03762 (2017).
[2] Dosovitskiy, Alexey, et al. "An image is worth 16x16 words: Transformers for image recognition at scale." arXiv preprint arXiv:2010.11929 (2020).
[3] Chen, Mark, et al. "Generative pretraining from pixels." International Conference on Machine Learning. PMLR, 2020.
[4] Liu, Ze, et al. "Swin Transformer: Hierarchical Vision Transformer using Shifted Windows." arXiv preprint arXiv:2103.14030 (2021).
[5] Ba J L, Kiros J R, Hinton G E. Layer normalization[J]. arXiv preprint arXiv:1607.06450, 2016.
[6] T.-Y. Lin, P. Dollar, R. Girshick, K. He, B. Hariharan, and ´ S. Belongie. Feature pyramid networks for object detection. In CVPR, 2017. 2, 4, 5, 7
[7] Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation[C]//International Conference on Medical image computing and computer-assisted intervention. Springer, Cham, 2015: 234-241.
[8] Bao, Hangbo, et al. "Unilmv2: Pseudo-masked language models for unified language model pre-training." International Conference on Machine Learning. PMLR, 2020.