This package is based on Gridap.jl to provide post-processing tools to calculate reconstructed fluxes associated to the given approximate solution of a PDE.
For simplicity, we consider here the Poisson equation
We suppose we have already computed a conforming approximation
The EquilibratedFlux.jl library then provides the tools to compute a reconstructed flux
associated to
This flux has the important property of being "conservative over faces" in the sense that
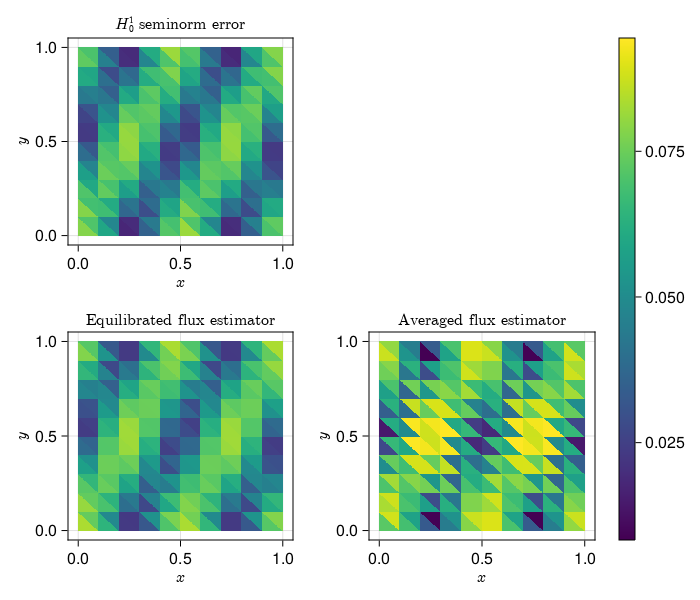
We provide two functions to obtain such an object:
build_equilibrated_flux
and
build_averaged_flux
both provide reconstructed fluxes, which we denote by
In addition to the properties listed above, the equilibrated flux
More details can be found in the documentation.
The reconstructed flux is the main ingredient in computing a posteriori error estimators.
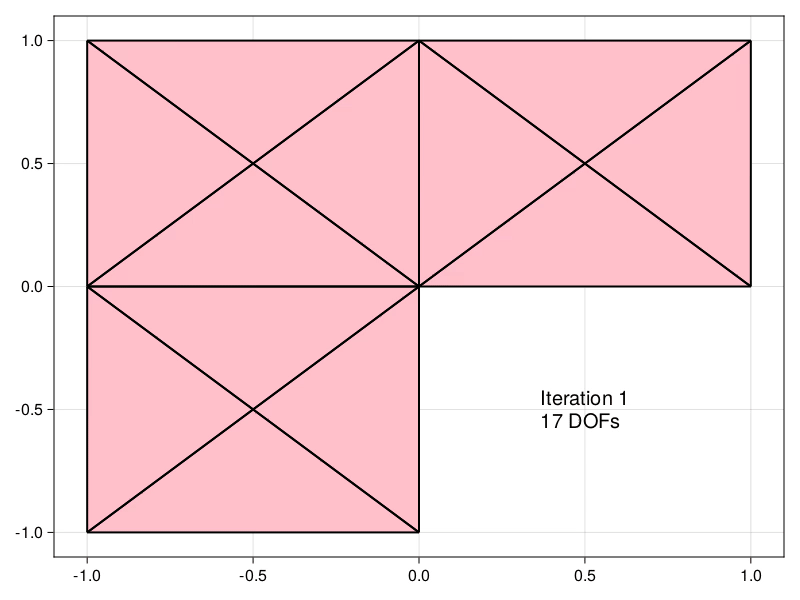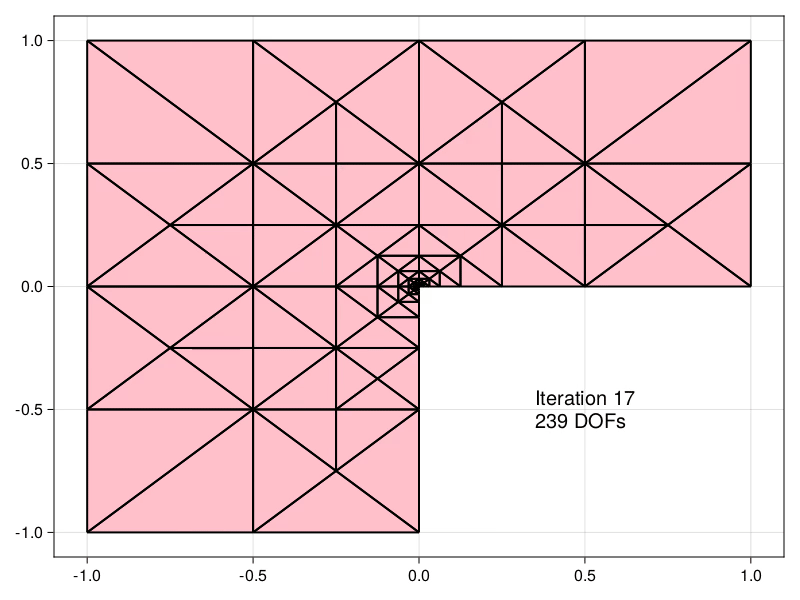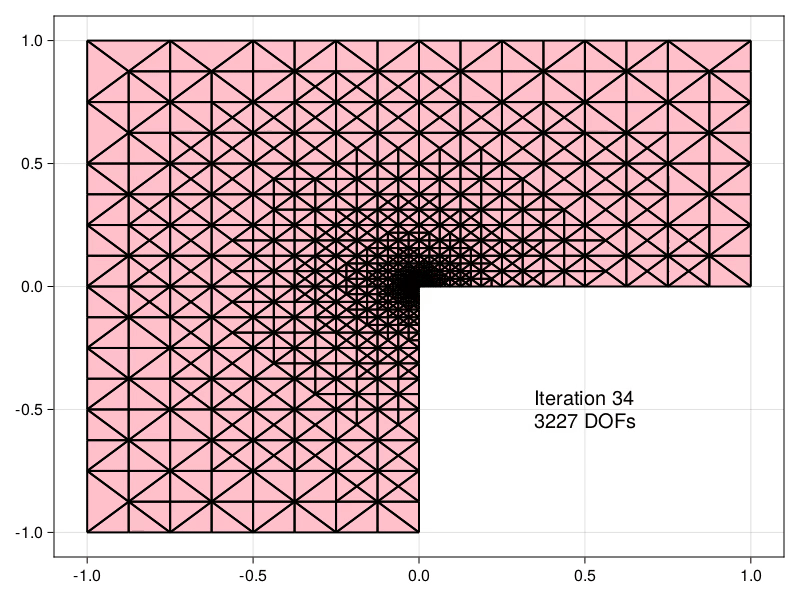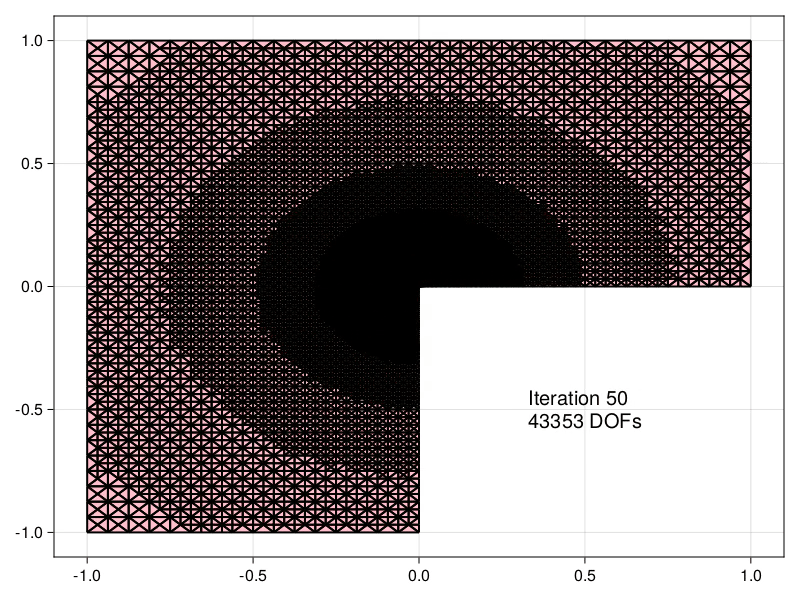
Estimators obtained using the equilibrated flux can be used to drive an Adaptive Mesh Refinement (AMR) precedure, demonstrated here for the Laplace problem in an L-shaped domain.