La ordenación o clasificación de datos (sort, en inglés) es una operación consistente en disponer un conjunto —estructura— de datos en algún determinado orden con respecto a uno de los campos de los elementos del conjunto. Por ejemplo, cada elemento del conjunto de datos de una guía telefónica tiene un campo nombre, un campo dirección y un campo número de teléfono; la guía telefónica está dispuesta en orden alfabético de nombres. Los elementos numéricos se pueden ordenar en orden creciente o decreciente de acuerdo al valor numérico del elemento. En terminología de ordenación, el elemento por el cual está ordenado un conjunto de datos (o se está buscando) se denomina clave.
La idea detrás del algoritmo de clasificación de burbujas es muy simple. Dada una lista desordenada, se comparan los elementos adyacentes en la lista y, después de cada comparación, colóquelos a la derecha en orden de magnitud. Esto funciona intercambiando elementos adyacentes si no están en el correcto orden. El proceso se repite n-1 veces para obtener una lista de n elementos. En cada iteración, el elemento más grande está dispuesto al final. Por ejemplo, en la primera iteración, el elemento más grande se colocaría en la última posición de la lista, y nuevamente, se seguirá el mismo proceso para los restantes elementos n-1. En la segunda iteración, el segundo elemento más grande será colocado en el penúltimo lugar de la lista, y el proceso se repetirá hasta que la lista se ordene.
Pseudocodigo:
bubbleSort(A, n)
Para i=1 hasta n -1
Para j=0 hasta i < n -2
Si (a[j]>a[j+1]) entonces
tmp=a[j]
a[j]=a[j+1]
a[j+1]=tmp
Fin Si
Fin Para
Fin Para
Fin bubbleSort
Ejemplo:
El algoritmo conocido como quicksort (ordenación rápida) recibe su nombre de su autor, Tony Hoare. La idea del algoritmo es simple, se basa en la división en particiones de la lista a ordenar, por ello se puede considerar que aplica la técnica "divide y vencerás". El método es, posiblemente, el más pequeño de código, más rápido, más elegante y más interesante y eficiente de los algoritmos conocidos de ordenación.
Este método se basa en dividir los n elementos de la lista a ordenar en dos partes o particiones separadas por un elemento: una partición izquierda, un elemento central denominado pivote o elemento de partición y una partición derecha. La partición o división se hace de tal forma que todos los elementos de la primera sublista (partición izquierda) sean menores que todos los elementos de la segunda sublista (partición derecha). Las dos sublistas se ordenan entonces independientemente.
Para dividir la lista en particiones (sublistas) se elige uno de los elementos de la lista y se utiliza como pivote o elemento de partición. Si se elige una lista cualquiera con los elementos en orden aleatorio, se puede elegir cualquier elemento de la lista como pivote, por ejemplo, el primer elemento de la lista. Si la lista tiene algún orden parcial que se conoce, se puede tomar otra decisión para escogerlo. Idealmente, el pivote se debe elegir de modo que se divida la lista exactamente por la mitad de acuerdo al tamaño relativo de las claves. Por ejemplo, si se tiene una lista de enteros de 1 a 10, 5 o 6 serían pivotes ideales, mientras que 1 o 10 serían elecciones “pobres” de pivotes.
Una vez que el pivote ha sido elegido, se utiliza para ordenar el resto de la lista en dos sublistas: una tiene todas las claves menores que el pivote y la otra, todos los elementos (claves) mayores o iguales que el pivote (o al revés). Estas dos listas parciales se ordenan recursivamente utilizando el mismo algoritmo; es decir, se llama sucesivamente al propio algoritmo quicksort. La lista final ordenada se consigue concatenando la primera sublista, el pivote y la segunda lista, en ese orden, en una única lista. La primera etapa de quicksort es la división o “particionado” recursivo de la lista hasta que todas las sublistas constan de sólo un elemento.
Algoritmo:
Inicio
Si lista tiene más de un elemento
Particionar la lista en dos sublistas (Sublista Izquierda y Sublista Derecha)
Aplicar el algoritmo QuickSort() a Sublist Izquierda
Aplicar Algoritmo QuickSort() a Sublista Derecha
Combinar las 2 listas ordenadas
Fin Si
FIN
Pseudocódigo:
QuickSort(A,p,r)
Inicio
Si p < r entonces // Si la lista tiene más de un elemento
q =Particionar(A,p,r)
QuickSort(A,p,q-1)
QuickSort(A,q+1,r)
Fin Si
Fin
Particionar(A,p,r)
Inicio
x=A[r]
i=p-1
para j=p hasta r-1
Si A[j]<=x
i=i+1
intercambiar A[i] con A[j]
Fin Si
Fin para
intercambiar A[i+1] con A[r]
retornar i+1
Fin
Ejemplo:
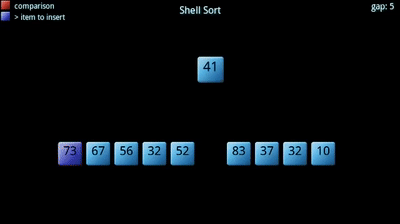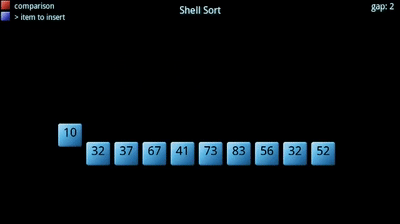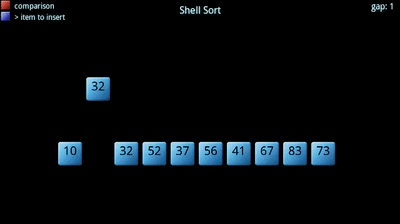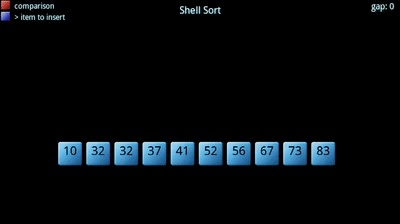
La ordenación Shell debe el nombre a su inventor, D. L. Shell. Se suele denominar también ordenación por inserción con incrementos decrecientes. Se considera que el método Shell es una mejora del método de inserción directa.
En el algoritmo de inserción, cada elemento se compara con los elementos contiguos de su izquierda, uno tras otro. Si el elemento a insertar es el mas pequeño, hay que realizar muchas comparaciones antes de colocarlo en su lugar definitivo.
El algoritmo de Shell modifica los saltos contiguos resultantes de las comparaciones por saltos de mayor tamaño, y con ello se consigue que la ordenación sea más rápida. Generalmente, se toma como salto inicial n/2 (siendo n el número de elementos), y luego se reduce el salto a la mitad en cada repetición hasta que sea de tamaño 1.
Ejemplo:
El método de ordenamiento Radix Sort también llamado ordenamiento por residuos puede utilizarse cuando los valores a ordenar están compuestos por secuencias de letras o dígitos que admiten un orden lexicográfico.
El algoritmo ordena utilizando un algoritmo de ordenación estable, las letras o dígitos de forma individual, partiendo desde el que está más a la derecha (menos significativo) y hasta el que se encuentra más a la izquierda (el más significativo). Nota: a cada letra o dígito se le asigna una llave o código representado por un número entero, el cual se utiliza para el ordenamiento de cada elemento que conforma el valor original.
Por ejemplo, se planea que una línea aérea proporciona números de confirmación diseñados con cadenas formadas con 2 caracteres donde cada carácter es un digito o una letra que puede tomar 36 valores (26 letras y 10 dígitos) y así hay 36^2 posibles códigos.
Para cada carácter de los 36 se genera un código numérico entero de 0-36.
carácter código
0 0
1 1
.
.
.
.
9 10
A 11
B 12
.
.
.
.
Z 36
Si se tienen los códigos de confirmación {F6,E5,R6,X6,X2,T5,F2,T3} y se utiliza un algoritmo de ordenación estable en el carácter que se encuentra más a la derecha se obtiene la lista parcialmente ordenada de códigos {X2,F2,T3,E5,T5,F6,R6,X6} . Ahora si se ordena utilizando el mismo algoritmo de ordenamiento estable, pero sobre el carácter que se encuentra más a la izquierda se obtiene la lista {E5,F2,F6,R6,T3,T5,X2,X6}.
Procesa las letras o dígitos de forma individual partiendo desde el digito menos significativo y hasta alcanzar el digito más significativo.
Si los códigos de confirmación se forman con 6 caracteres y se tiene la lista de códigos {X17FS6,PL4ZQ2,JI8FR9,XL8FQ6,PY2ZR5,KV7WS9,JL2ZV2,KI4WR2}, el ordenamiento del carácter más a la derecha hacia el de más a la izquierda se muestra.
El algoritmo en pseudocódigo del Radix Sort es:
RadixSort(A,d)
Inicio
Para i=1 hasta i=d
Ordenamiento de A en el digito i
Fin
Donde A es una lista de n elementos, d es el número de dígitos o caracteres que tienen los elementos de A, si i = 1 se refiere al dígito o carácter colocado más a la derecha y cuando i = d al que está más a la izquierda. El ordenamiento se realiza con algún algoritmo estable como por ejemplo Counting Sort.
Merge Sort es un algoritmo de ordenamiento basado en el paradigma divide y vencerás o también conocido como divide y conquista. Esta es una técnica de diseño de algoritmos que consiste en resolver un problema a partir de la solución de sub-problemas del mismo tipo, pero de menor tamaño. Consta de tres pasos: Dividir el problema, resolver cada sub-problema y combinar las soluciones obtenidas para la solución al problema original
Las tres fases en este algoritmo son:
Divide: Se divide una secuencia A de n elementos a ordenar en dos sub-secuencias de n/2 elementos. Si la secuencia se representa por un arreglo lineal, para dividirlo en 2 se encuentra un número q entre p y r que son los extremos del arreglo o sub-arreglo. El cálculo se hace q = | (p + r) / 2 |.
Conquista: Ordena las dos sub-secuencias de forma recursiva utilizando el algoritmo MergeSort(). El caso base o término de la recursión ocurre cuando la secuencia a ser ordenada tiene solo un elemento y éste se supone ordenado.
Combina: Mezcla las dos sub-secuencias ordenadas para obtener la solución. El algoritmo es:
1. Ordenar una secuencia S de elementos:
1. Si S tiene uno o ningún elemento, está ordenada
2. Si S tiene al menos dos elementos se divide en dos secuencias S1 y S2, S1 conteniendo los primeros n/2, y S2 los restantes.
3. Ordenar S1 y S2, aplicando recursivamente este procedimiento.
4. Mezclar S1 y S2 ordenadamente en S
2. Mezclar dos secuencias ordenadas S1 y S2 en S:
1. Se tienen referencias al principio de cada una de las secuencias a mezclar (S1 y S2).
2. Mientras en alguna secuencia queden elementos, se inserta en la secuencia resultante (S) el menor de los elementos referenciados y se avanza esa referencia una posición.
Fuente:
Baka, B. (2017). Python Data Structures and Algorithms. Birmingham, Reino Unido: Packtpub.
Cormen, T. (2013). Algorithms Unlocked. Cambridge: IT Press.
Cormen, T., Leiserson, C., Rivest, R., & Clifford, S. (2009). Introduction to Algorithms. Cambridge: The MIT Press.
Joyanes-Aguilar, L., & Zahonero-Martinez, I. (2008). Estructuras de datos en Java. Madrid, España: McGraw-Hill.